Vivimos en un mundo donde no sólo el comportamiento humano es una sorpresa. La Naturaleza acompaña esta incertidumbre con la intensidad de los huracanes, la intermitencia de ondas de calor, frío y lluvia. El desierto de Atacama se cubre de flores mientras Siberia se descongela. 

La necesidad de predecir con una mayor precisión el efecto del aumento en la concentración de dióxido de carbono en la atmósfera terrestre ha motivado la aplicación de una gran variedad de métodos y conceptos al estudio del clima. 

Aún cuando se tienen modelos confiables para una gran variedad de fenómenos, estos presentan errores al simular el comportamiento de la atmósfera. En particular, esto motiva la búsqueda de estructuras a partir de las cuales puedan reconocerse patrones en la intensidad y dirección de las corrientes de aire. 

En uso reciente de ideas que provienen de la Geometría Hiperbólica en la búsqueda de estas estructuras muestra cómo aún las teorías más abstractas pueden volver al mundo del que surgieron como representaciones para proponer soluciones a problemas en el estudio del calentamiento global. 

Asimismo, esta aplicación nos lleva a preguntarnos si otros elementos técnicos utilizados en esta teoría pueden inspirar criterios de evaluación de la estabilidad del sistema climático.

El movimiento y la forma

Una partícula se desliza en el agua, gira y avanza a través del océano bajo el sol de mediodía. Podría ser una molécula de agua o un alga unicelular que acabará en el estómago de una ballena. La trayectoria que recorre tiene la restricción de la forma del espacio. 

De no encontrar obstáculos, seguirá la dirección y velocidad de su impulso inicial. Si es un rayo de luz, dibujará el camino con la menor distancia entre dos puntos. En este caso, la línea que traza su recorrido es llamada geodésica. En el caso de una región de unos cuantos metros, será una recta, como podemos ver en el haz de líneas blancas que entra por la ventana del cuarto en el que leemos este texto.

Sin embargo, en observaciones astronómicas, la luz viaja distancias mucho mayores; por ejemplo, entre la Tierra y la estrella Sirius (≈8.57 años luz), el espacio se pandea y se formarán entre ellas y cualquiera otra, los lados arqueados de un triángulo cuyos ángulos internos son menores a los habituales y suman una cantidad menor a 180 grados [Mil97]. 

Si, en lugar de tres objetos, tenemos una constelación; podemos subdividirla para estudiarla en tríadas más simples; y considerar a los triángulos como las figuras básicas, pero al deslizarlos a través del espacio, podrían distorsionarse. Su forma es determinada por la magnitud de sus lados y ángulos; y se preserva solamente si la curvatura del espacio es uniforme, para que al llevar la figura de un sitio a otro no se modifique. 

De otro modo, se convierte en una casualidad, un fenómeno irrepetible determinado por la localización exacta de la figura; y las propiedades encontradas en ella no serán suceptibles de utilizarse en ninguna otra.

Forma y curvatura

La curvatura de una línea en un punto fue definida por Carl Friedrich Gauss (1777-1855) como el radio de la circunferencia más parecida a ella en ese lugar. En el trabajo titulado Investigaciones Generales sobre Superficies Curvas, publicado en 1827, Gauss mostró que la curvatura Gaussiana y la manera de medir longitudes sobre ella son proporcionales.

Es decir, si nos desplazamos sobre un relieve y queremos tomar la dirección que nos lleve por la ruta más corta, podríamos hallarla con una brújula que apuntara a un norte cambiante por donde hay menos inclinación. Una de las consecuencias, como demostró Eugenio Beltrami (1835-1900) en 1868, es que el criterio de congruencia de figuras —dos ángulos rectos siempre son iguales— sólo es válido en superficies cuya curvatura es constante porque
de otro modo nos encontraríamos en el salón de los espejos, nuestro reflejo cambiaría a cada paso y perderíamos la capacidad de reconocernos a través de él.

Si volvemos al cuarto en el que leemos, la luz viaja en línea recta y la curvatura es cero en todas partes. En este caso, las cualidades de las figuras que nos rodean se deducen de los cinco postulados de la Geometría Euclidiana.
Al dividirlas en triángulos para estudiarlas, la suma de sus ángulos internos es siempre igual a π. 

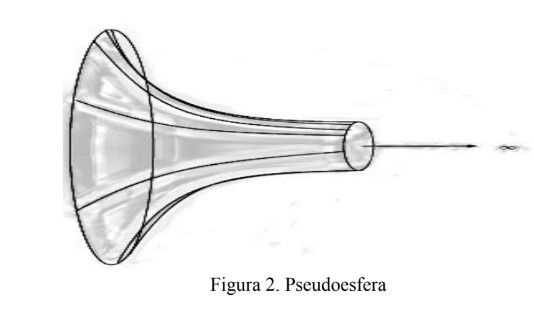
Si alejamos los extremos de la escena y observamos la Tierra desde la Luna, las geodésicas serán arcos de circunferencias que pasan por los polos, curvas que se cierran sobre sí mismas. En cambio, un espacio donde pueden formarse triángulos cuyos ángulos internos suman menos de 180 grados, se abre, como sucede en la superficie de curvatura constante -1 llamada pseudoesfera, que se ilustra en la Figura 2.

La Geometría Hiperbólica y la Naturaleza

El problema de determinar si el quinto axioma de la Geometría Euclidiana era consecuencia de los cuatro anteriores condujo al descubrimiento independiente de una nueva teoría, la Geometría
Hiperbólica por parte de Nicolai Ivanovich Lobachevsky (1792-1856), János Bolyai (1802-1860) y Gauss.

La hipótesis de Lobachevsky fue cambiar la manera de medir; y de esta manera, obtener una representación mejor de la forma como se manifiesta en cualquier escala [Lob86]: «Me he propuesto probar, por medio del Análisis, que nadie está autorizado, más que por observaciones directas, asuponer que la suma de los ángulos internos de un triángulo rectángulo es igual a dos ángulos rectos; y que la Geometría no puede existir sino en la Naturaleza».

En el mismo artículo de 1868, Beltrami probó que las superficies de curvatura constante negativa, como la pseudoesfera, son lugares concretos que funcionan bajo las reglas de la Geometría Hiperbólica; es decir, las propiedades de sus figuras pueden inferirse de los nuevos principios planteados.

Ahora, el cuarto se ha extendido y tiene esquinas en varias estrellas. El haz de luz que lo atraviesa parece más una cascada que un rayo. Si una nave viajara sobre él, necesitaría un mapa. Una manera de
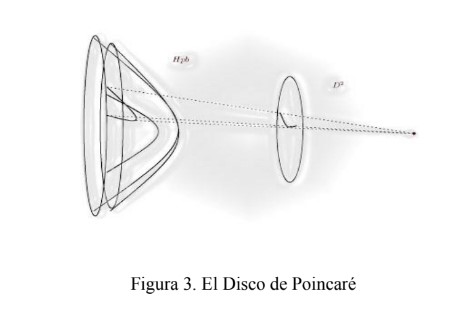
obtenerlo es proyectar cada punto hacia un disco plano de radio 1, el Disco de Poincaré, como se muestra el la Figura 3. 

En el mapa, la distancia total de la travesía debe coincidir con aquella transitada en el espacio original. Es decir, el mapa debe ir acompañado de una regla de cálculo de magnitudes. En consecuencia, en el Disco de Poincaré, una geodésica se convierte en el arco de una circunferencia ortogonal al perímetro o un segmento de diámetro, ilustrados en la Figura 4. Así, un polígono regular en el disco suele tener lados curvos. Si tiene más de cuatro lados, al pegarlos como si se cosiera con él una pelota, se obtienen otros espacios, las superficies hiperbólicas compactas, en donde se construyen los ejemplos clásicos de los sistemas estables.

Geometría Hiperbólica y Cambio Climático

Podemos volver a la partícula inicial. La fuerza que la impulsa a través del agua sigue leyes que suelen ser expresadas en forma de ecuaciones, cuya solución lleva consigo una serie de dificultades. Henri
Poincaré (1854-1912) propone un planteamiento distinto al cálculo de los valores numéricos de posición y velocidad que puede tener: el estudio geométrico de sus trayectorias.

Por ejemplo, una partícula que regresa a su punto de partida formará una curva cerrada, un ciclo, y ser á distinta de una que se aleja sin volver. Así surge el concepto de sistema dinámico como el conjunto de las trayectorias recorridas por los puntos de un espacio. Una imagen utilizada para visualizarlo es una gota de tinta que cae en un vaso de agua y se desbarata en espirales que hace visibles las corrientes de líquido.

Si sacudimos el vaso, los vórtices desaparecen; pero, ¿qué sucede con las corrientes principales en el océano? La experiencia nos dice que hay sistemas que pueden ser alterados sin perder sus ciclos
naturales. En 1965, Dmitri Victorovich Anosov demostró que un sistema estable es aquél donde el espacio se divide en dos zonas: una de aceleración y otra de desaceleración [Anv69]. 

Los ejemplos que se presentan en el trabajo de Anosov son precisamente sistemas formados por curvas geodésicas en superficies de curvatura negativa constante; y se estudian como objetos pertenecientes a la Geometría Hiperbólica. Ahora, si bien la aplicación de este resultado no es inmediato, la importancia de tener una caracterización de la estabilidad como una propiedad explícita está en la posibilidad de desarrollar criterios que permitan distinguirla en otros contextos.

Si imaginamos que la zona de aceleración del líquido es roja y la de desaceleración es azul, podemos escoger una curva en cada una. Si estas se cruzan, el punto en el que lo hacen es llamado punto hiperbólico. 

El él pueden observarse simultáneamente la intensidad de la velocidad en cada región y distinguir un esqueleto formado por la red de curvas rojas, azules y nodos. Con base en esta idea, en el año 2000, G. Haller y G. Yuan introdujeron el concepto de estrucuturas Lagrangianas coherentes [Hal00], a partir de las cuales se han desarrollado recientemente métodos de detección de patrones en fluídos turbulentos de aire [Ols13], [Tan10]; lo que nos lleva a preguntarnos, ¿qué otras cualidades de los sistemas estables pueden señalarnos medidas para analizar, entender, evaluar y monitorear el sistema climático?

____________________________________________

Dra. Carla Valencia Negrete, Académica de Tiempo Completo del Departamento de Física y Matemáticas de la IBERO

Bibliografía

[Anv69] D. V. Anosov, Geodesic Flows on Closed Riemannian Manifolds with Negative Curvature, Proceedings of the Steklov Institute of Mathematics, AMS, 1969.

[Hal00] G. Haller, G. Yuan, Lagrangian coherent structures and mixing in two dimensional turbulence, Physica D, 147 (2000) 352-370.

[Lob86] N. I. Lobachevsky, Géométrie Imaginaire, Collection Complète des Œvres Géometriques de N. I. Lobatcheffsky, Édition de l'Université Impériale de Kasan, Tome Seconde, 1886, pág. 590.

[Mil97] J. W. Milnor, Hyperbolic Geometry: The First 150 Years, Bulletin of the American Mathematical Society, 6 (1982), pág. 9-14.

[Ols13] M. J. Olascoaga et al., Drifter motion in the Gulf of Mexico constrained by altimetric Lagrangian coherent structures, Geophys. Res. Lett., 40 (2013) 6171-6175.

[Tan10] W. Tang, M. S. Mathur & G. Haller, Lagrangian Coherent Structures near a Subtropical Jet Stream. Journal of The Atmospheric Sciences-J ATMOS SCI. 67 (2010) 2307-2319.